Статистический анализ данных

Как научный опыт и математические формулы помогают определить закономерности, построить модели для прогнозирования будущего и управлять любым проектом, в том числе в IT?

Как правильно строить модели?

Модель — это отображение, проекция реального мира, которая упрощает его, стандартизирует, описывает качественными и количественными характеристиками и позволяет нам строить прогнозы о дальнейшем его развитии.

Любая модель — от модели гравитации до модели женской красоты — предназначена для того, чтобы досконально описывать происходящие явления и отражать этот сложный мир более понятным образом.

Чтобы построить модель чего угодно, недостаточно просто хорошо подумать об этом — наше сознание обязательно добавит в модель когнитивные искажения и сделает эту модель субъективной и некорректной.

Главный критерий качества любой модели — это её воспроизводимость. Если вы смогли построить модель, которую с учетом определенных ограничений другой человек может повторить и использовать при схожих обстоятельствах, модель можно считать удачной. Самые наглядные сферы, в которых максимально строго подходят к построению и выборам модели – космонавтика и медицина. На другом конце этого спектра – астрология и предсказания, которые не могут опереться ни на какую воспроизводимую модель.

Не важно, что вы разрабатываете — лекарство или формулу торговли на фондовом рынке, результат от использования модели должен быть идентичным у всех, кто её воспроизводит.

Как проводить измерения?

Ничего нельзя измерить с абсолютной точностью — любое измерение имеет погрешность.

Два объекта объёмом 50 и 52 литра будут считаться равными в пределах погрешности, если у одного объекта диапазон погрешности 50л +/-8л, а у второго 52л +/-6л.

Формула определения погрешности выглядит так:

Чтобы измерить уже несколько величин и вывести их среднее значение — например, средний объём ста похожих объектов — используют распределение по Гауссу или нормальное распределение.

Распределение по Гауссу позволяет описать диапазон значений с помощью среднего значения и стандартного отклонения. Схематично это распределение выглядит как купол, пиком которого является среднее значение — в нашем случае средний объём всех измеряемых объектов.

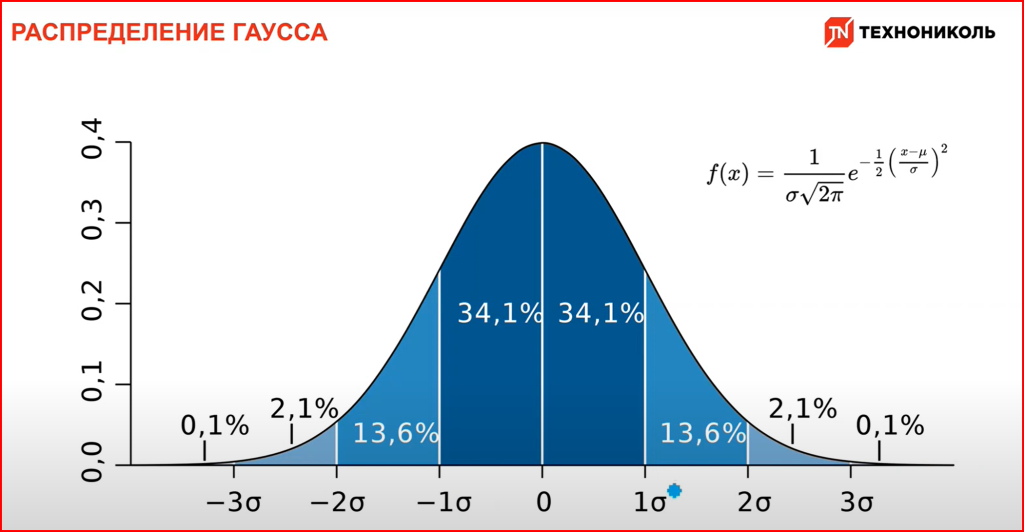
Ширина купола определяется сигмой – величиной стандартного отклонения – и зависит от того, насколько разбросаны значения случайной величины. Чем больше стандартное отклонение, тем больше разброс значений и тем меньше точность оценки среднего значения. Например, если стандартное отклонение больше, то вероятность того, что наблюдаемое значение будет значительно отличаться от среднего, также будет больше.

Чтобы сузить «купол» нормального распределения и сделать статистические измерения более точными, необходимо увеличивать n, то есть число измерений. Чем уже купол, тем ниже отклонение и точнее диапазон возможных значений.

Хорошая статистика — та, в которой достаточное количество измерений n и ниже погрешность.

Чаще всего из нематематических специалистов с такого рода данными, измерениями, выборками приходится работать HR-специалистам, и результаты их деятельности — модель, основанная на измерениях текучки, среднего возраста, среднего уровня зарплаты, применяется для управления коллективом.

Ошибки при построении моделей

Математические знания необходимы для того, чтобы построить качественную модель, способную решать конкретную бизнес-задачу. Как правило требования к точности моделей растут в период финансовых ограничений — например, во время кризиса.

Ошибка 1.

Очень часто среднее значение само по себе может кардинально отличаться от среднего значения с погрешностью. Из-за этого модель, которая казалась точной и результативной, на самом деле может давать непредсказуемые результаты.

На одном из проектов ТЕХНОНИКОЛЬ команда столкнулась с задачей: посчитать, за какой период клиент повторно возвращается за заказом продукта. Среднее время такого повторного заказа было 4 недели, но среднее время с погрешностью составляло 4 недели +/-5 недель. То есть с вероятностью выше 90% клиент совершает заказ не через месяц, а в течении 2 с лишним месяцев, что снижает потенциальную выгоду компании.

Ошибка 2.

Во время анализа модели нам часто кажется, что если какой-то ресурс умножить на Х, его производительность также увеличится в Х раз — например, если мы удвоим команду, скорость разработки тоже удвоится.

Люди склонны считать, что большинство зависимости в нашем мире носят линейный характер. Линейную регрессию, или линейную зависимость, можно применять только в тех ситуациях, в которых мы экспериментально установили зависимость одной переменной от другой.

Ошибка 3.

Иногда выборка среднего значения какого-то бизнес-показателя — например, возвратности клиентов — скрывает реальную картину. Вернёмся к кейсу ТЕХНОНИКОЛЬ с показателем возвратности покупателя 4 недели. Мы взяли среднее значение, но что, если на самом деле наш диапазон выглядит так?

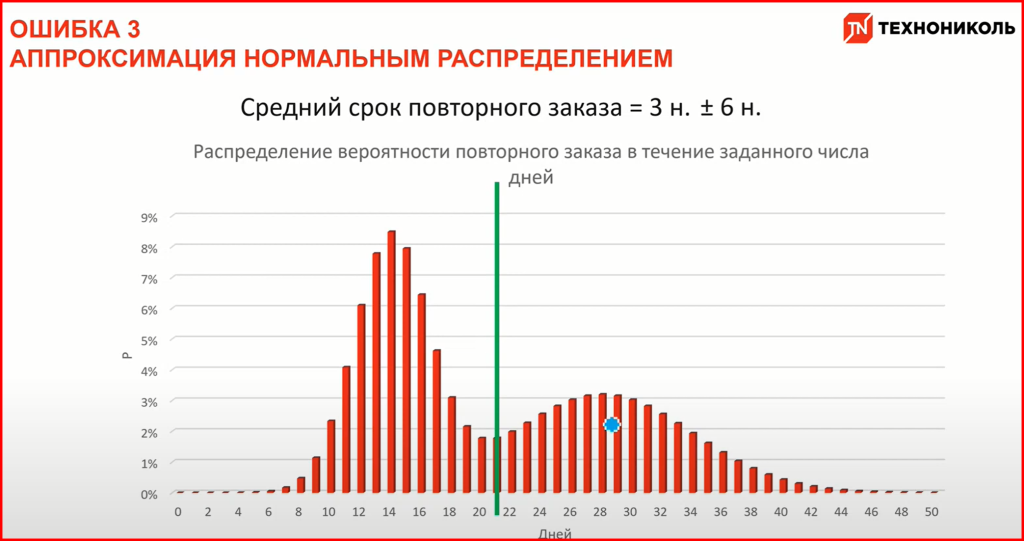
Мы видим 2 разных аудитории с разным периодом заказа: одна аудитория делает повторный заказ через 4 недели, вторая — через две недели. С ними нельзя работать одинаково и рассчитывать погрешность как среднее значение— нужно сегментировать группы и находить для каждой свои препятствия и ограничения. Опираясь на среднее значение, мы не попадём ни в одну из аудиторий и будем строить свою стратегию вхолостую.

Ошибка 4.

Игнорирование систематических погрешностей. Самый частый способ анализа— сбор хронологии показателей — сложно измерить корректно. Влиять на показатели месяца или квартала может всё, что угодно — от сезонности до изменения операционной системы в телефоне пользователей, из-за которого может ломаться мобильное приложение.

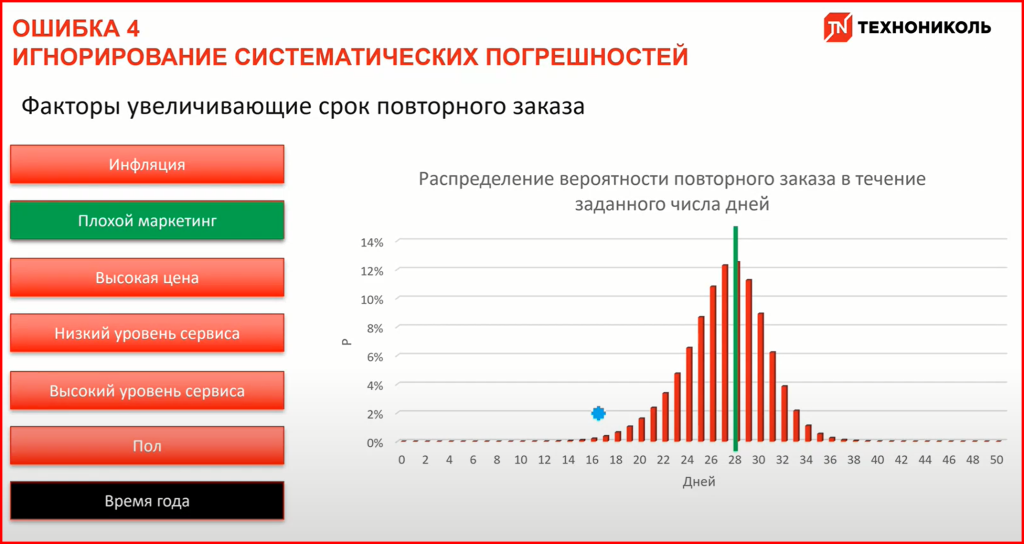
Чтобы найти негативные факторы, реально влияющие на бизнес, необходимо проводить клинические исследования, или A/B тесты. Попробуйте разделить аудиторию на 2 группы — одну из них оставьте без изменений, а на другой тестируйте гипотезы. Сравнивайте влияние только одного фактора — если во второй группе после теста результаты улучшились, значит, фактор работает.

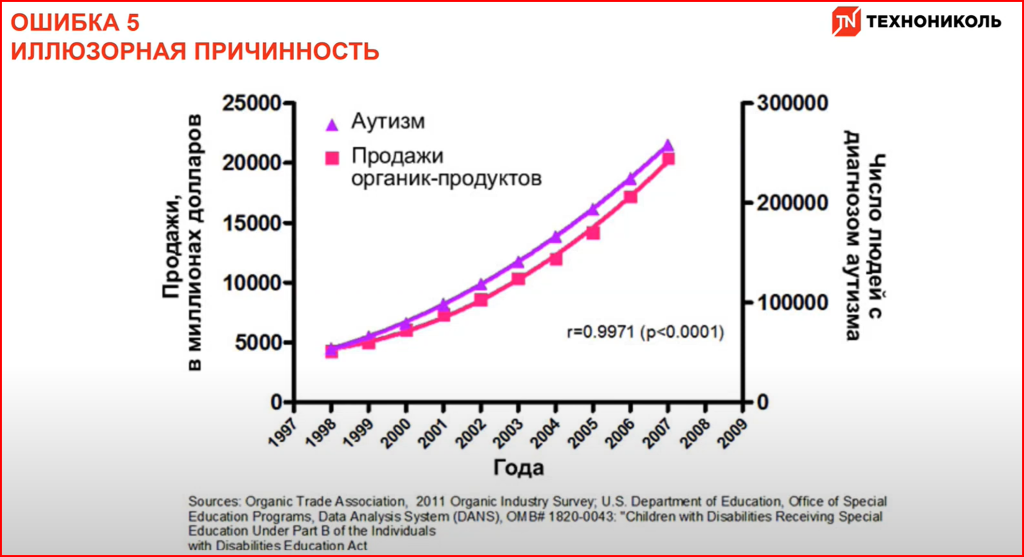
Ошибка 5.

Если мы видим на графике 2 кривые, которые идут вместе или имеют похожую динамику, нам кажется, что одно событие или явление следует из второго. Это может означать, что второй фактор идёт за первым, но совсем не означает причинно-следственную связь. Чтобы установить, есть ли она, нужно также проводить эксперимент с аудиторией и делить её на 2 группы — в одной группе потенциальную причину убирать, а в другой оставлять и по истечении некоторого срока смотреть, какая пара кривых у нас получается.

Из-за незнания всех этих факторов бизнес продолжает жить и действовать на автомате, используя «интуитивную» статистику.

Когнитивные искажения, которые мешают работать со статистикой

Человеческий мозг легко работает с пропорциями. Представьте себе половину от единицы или 20% от 50 — у вас это легко получится. Но почти невозможно представить себе что угодно в степени экспонента в квадрате — люди не умеют визуализировать возведение в степень и извлечение корня.

Самое неудобное, что среднестатистический человек не умеет работать со статистикой и вероятностями, потому что в теории вероятности пропорций очень мало, а в основном зависимость определяется степенями.

Феномен «Баадера-Майнхоф»

Посмотрите на эту последовательность цифр.

00111111111111111100111100

Первое, на что большинство обращает внимание — слишком большое количество единиц. Из-за этого последовательность не кажется случайной, но на самом деле она сгенерирована рандомным сочетанием нулей и единиц. Это искажение — феномен «Баадера-Майнхоф», которое возникает при анализе данных. Его суть в следующем: если мы анализируем группу схожих событий, которые появились недавно, примерно в одно и то же время, мы начинаем считать их частыми.

Иногда случайности группируются по неизвестным причинам — 2 или 3 случайных поломки приложения подряд не обязательно свидетельствуют о том, что система слабая. Эти поломки вполне могут быть вызваны абсолютно разными причинами и произойти с интервалом год, 2 года или не произойти вовсе.

Ошибка в духе техасского стрелка или эффект обратного результата

Взгляните на эту картинку. Кажется, что стрелок, который бил в эту мишень, очень меткий.

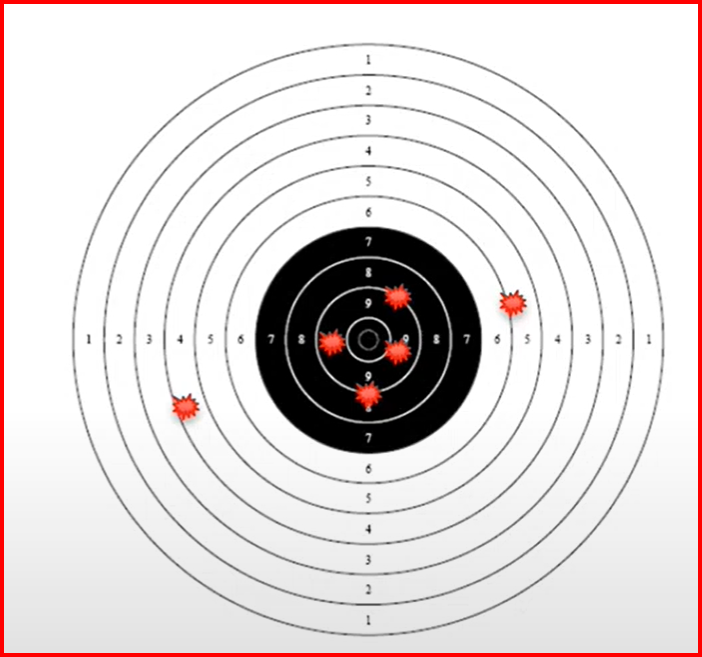
Но что, если изначально мишень и выстрелы были расположены вот так?

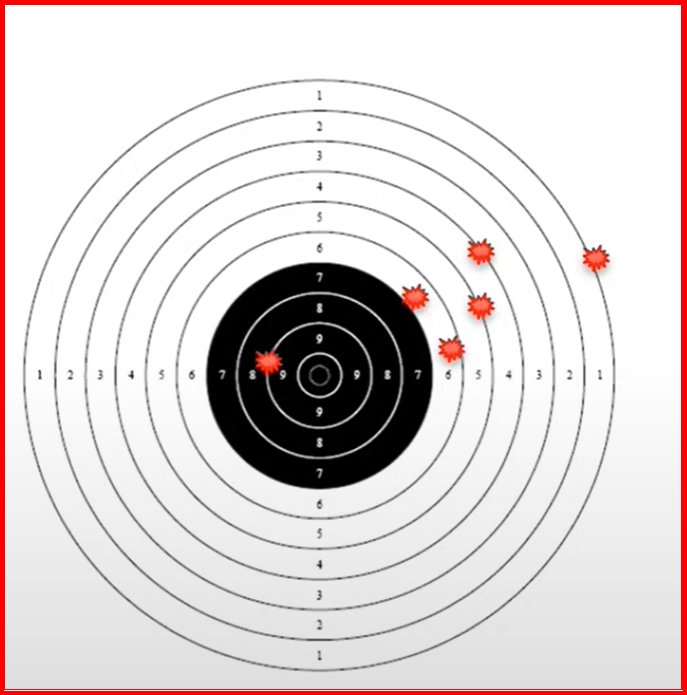
Это искажение названо так в честь реального стрелка из Техаса, который так обманывал своих друзей – рисовал мишень вокруг уже сделанных выстрелов.

Это искажение — та причина, по которой опасно собирать всю аналитику до построения гипотез. Вы не должны строить ожидания на основе данных, которые получили, потому что корреляция, которую вы могли там заметить, может отсутствовать. Нужно строить ожидания заранее и только потом смотреть данные — сначала рисуем мишени, потом стреляем, а не наоборот.

Ошибка выжившего

Приведём хрестоматийный пример с американскими самолетами, которые во время Второй мировой войны летали в Германию. Их часто сбивали, и многие самолёты не возвращались. Тогда появилась задача точечно укрепить самолет, чтобы он не был сбит, но не бронировать его целиком — двигатель бы не справился.

Для этого были проанализированы самолеты, которым все-таки удалось вернуться. Чаще всего у таких самолётов находили повреждения в крыльях, поэтому решили укрепить именно их. Но со временем процент сбитых самолетов с бронированными крыльями только увеличился.

Уже после войны стало ясно: не возвращались обратно самолёты, которым стреляли в фюзеляж. Повреждения крыльев оказались не критичными, зато именно фатальные попадания в фюзеляж не смогли учесть при анализе.

Статистику сформировали выжившие – те, кому не повезло оказаться живым, в неё не попали.

На эту ошибку очень легко наткнуться в бизнесе, но в менее явном виде — например, когда вы анализируете активную пользовательскую аудиторию.

Обобщение частных случаев

Мы часто сталкиваемся с ним, когда из опроса небольшой группы людей пытаемся сделать выводы об общей ситуации и распространить эти выводы на широкую аудиторию. В научном исследовании существуют способы доказать репрезентативность фокус-группы, но это долгий и сложный процесс, который охватывает выборку не 20-30 человек, а 20-30 тысяч. Маркетинговое исследование, пусть даже для очень большой компании, на такое пока не способно.

Предвзятость подтверждения

Вспомните себя во время спора — наверняка у вас был соблазн специально начать искать факты, которые поддерживают вашу точку зрения, не обращая внимания на истину. Это искажение называется предвзятостью подтверждения и в совокупности со всем вышеописанным может привести к очень неприятным результатам, когда мы принимаем решение и в дальнейшем видим только подтверждение этого решения.

Эффект авторитета

Это явление, когда люди автоматически приписывают человеку, который успешен в одной области, успешность в других областях. Например, если человек является хорошим спортсменом, мы можем считать, что он также хорошо пишет картины, даже если это не так. Это явление часто встречается в рекламе, когда знаменитости используются в качестве лиц бренда, но в науке его стараются избегать.

Профессионально ставить KPI очень трудно — нужно быть хорошим управленцем и одновременно отличным математиком, чтобы модель, которую ты строишь для целого подразделения или филиала компании, была эффективной.

Классический пример плохого KPI — «увеличить количество активных пользователей на 10% к следующему месяцу». К такому методу постановки KPI сразу есть вопросы:

• кто считается пользователем? Что этот человек должен сделать: посетить сайт или зарегистрироваться, сделать заказ или оставить номер телефона?
• как посчитано число пользователей в прошлом месяце? Возможно, за этот месяц часть клиентов сменила номера и потеряла доступ к аккаунту или наоборот зарегистрировала второй, третий или пятый аккаунт;
• почему KPI считается помесячно? Соответствует ли это стандартному циклу поведения вашей аудитории? Опять вспомним кейс ТЕХНОНИКОЛЬ со сроком заказа до 9 недель — для такого периода нет смысла считать цикл помесячно, если пользователь может вернуться в произвольный момент времени в течение 2,5 месяцев;
• что делать с некачественными пользователями, которых нужно было нагнать «для галочки» и которые будут ухудшать статистику по активности и заказам?
• как учитывать в статистике случайных «чёрных лебедей» — непредсказуемые влияющие на результат события?

Можно привести примеры много других факторов, влияющих на спрос – например, сезонное изменение цен, смену общей картины потребления и так далее. Хотя каждый из них по отдельности может казаться незначительным, в совокупности получается недостижимый KPI, основанный на плохой модели.

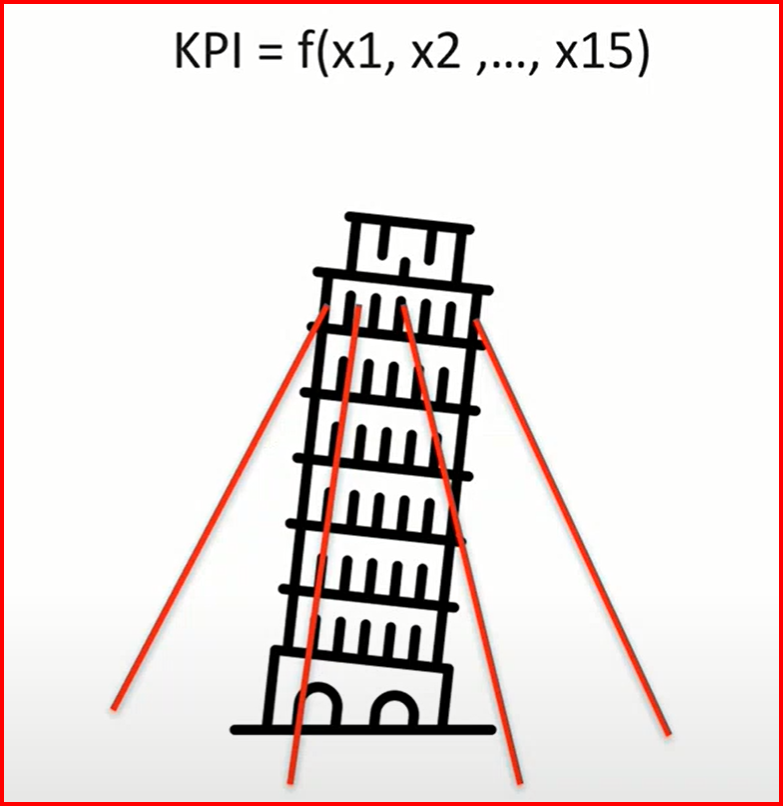
Хороший KPI выглядит как башня, которая держится на нескольких тросах. Все они должны быть взаимодополняющими – если стоит цель увеличить число зарегистрированных пользователей, нужно предусматривать меры, повышающие качество этих пользователей, чтобы KPI по активности не отклонились в сторону и башня не упала.

Выводы

1) Если вы работаете с цифрами, изучите основы математической статистики. К сожалению, мы не можем игнорировать наши когнитивные искажения — так устроен человеческий мозг. Единственный способ реже сталкиваться с искажениями — это знать и использовать математику.

2) Не верьте своей интуиции. Теория вероятности полностью контринтуитивна.

3) Смотрите в суть показателей. Не нужно просто брать среднее значение — оно может ничего не означать или даже ввести вас в заблуждение.

4) Не «играйте» с графиками, определяйте индикаторы оценки заранее. Желание построить гипотезы на основе готовых графиков — это очень плодородная почва для когнитивных искажений.

5) Не обманывайтесь и не обманывайте других. Если вы пишете отчёт или рисуете график, обязательно учитывайте погрешность.

6) Помогайте коллегам. Объясняйте, что одно число ничего не значит, если рядом не написана погрешность. Доказывайте, что рост на 2% в пределах погрешности +/- 5% — это не повод менять стратегию и перекраивать бюджет.

7) Используйте безотказный повод прогнозирования. Если перед вами стоит срочная задача, по которой вы не успеваете собрать правильную статистику и провести эксперименты, положитесь на random.org. Просто задайте ему диапазон значений — он быстрее вас справится с задачей, а точность прогноза будет такой же.